Overview
This page describes how to calculate faces for a geodesic sphere, starting with any primitive with triangular faces (e.g. a tetrahedron, octahedron, or icosahedron).
The theoretical method for locating the vertices is described here. However, it's a bit of a jump to go from knowing how to find the vertices by hand to being able to calculate the face triplets programmatically.
Working with Vectors
We start with where the hand algoritm leaves off, with a triangular face subdivided into sub triangles. (Here, the frequency is 7.)
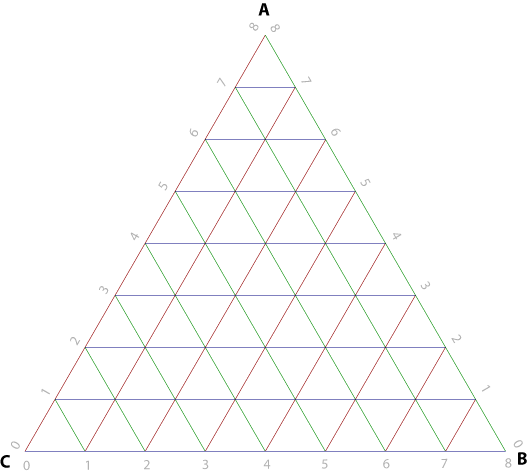
Because the sides were divided into equal pieces, we can use a vector to describe a step in each direction:
Each of these vectors are created by finding the difference between the points, and dividing it by (frequency + 1):
x = ( B - C ) / (frequency+1) y = ( A - C ) / (frequency+1) s = ( A - B ) / (frequency+1)
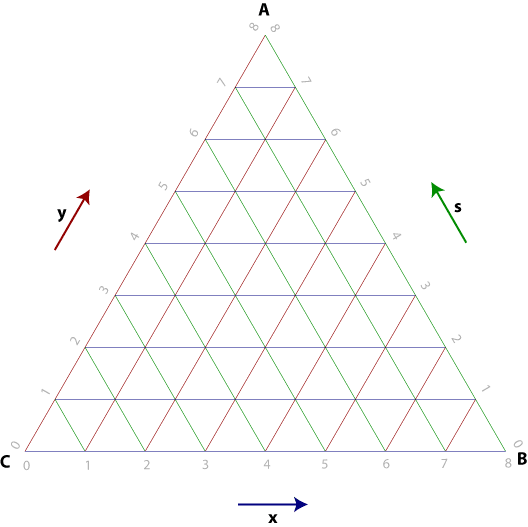
Every point in the face can be described as a combination of x, y, and s steps. However, while the presence of the s vector is convenient for stepping around, it's useful to note that it's not needed. The s stands for 'sidestep': one step in the s direction can be seen as one step in the y direction minus one step in the x direction. This may be easier to see if we change the initial points of the triangle:
The point arrived at in the above can be represented as 3x + 2s + 1y, or simply 1x + 3y. While easy to see, the formula is s = y - x, so 3x + 2s + 1y = 3x + 2(y - x) + 1y = 1x + 3y. This allows us to uniquely identify every vertex point.
Bounds of the Plane
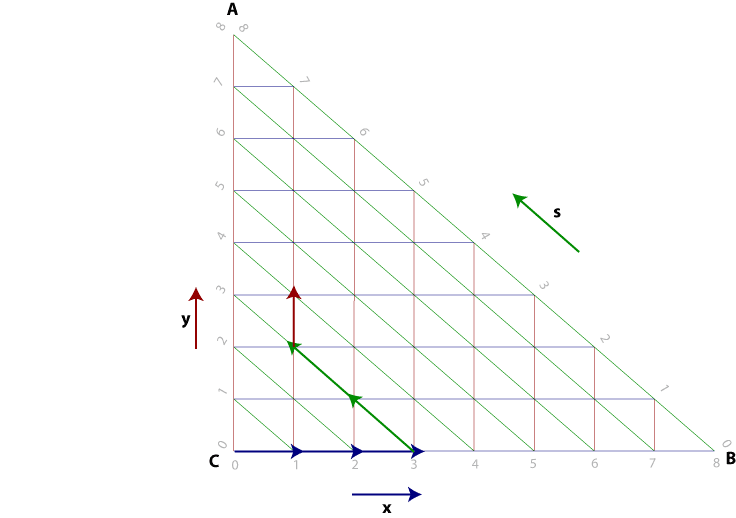
Using only x and y steps to reference points, we need to be able to tell which points are within the bounds of the triangle, and which are out of bounds. It's easy to see from the previous diagram that if x_steps or y_steps is less than 0, the point is off the face. But what about the third side?
If we look at the x/y coordinates for points along the third side...
(0,8) (1,7) (2,6) (3,5) (4,4) (5,3) (6,2) (7,1) (8,0)
...it becomes clear the sum of coordinate points add up to 8. So the criteria for a coordinate to be in the triangle's bounds are:
in_bounds? = (x_steps >= 0) && (y_steps >= 0) && ( x_steps+y_steps <= (frequency+1) )
Finding All Faces
So, now that we have an easy way to talk about points on the face, and determine if they're in the face or not. Now we need to actually be able to programmatically find them all.
The technique I use is to first recognize that the plane of triangles can be turned into a series of adjacent hexagons:
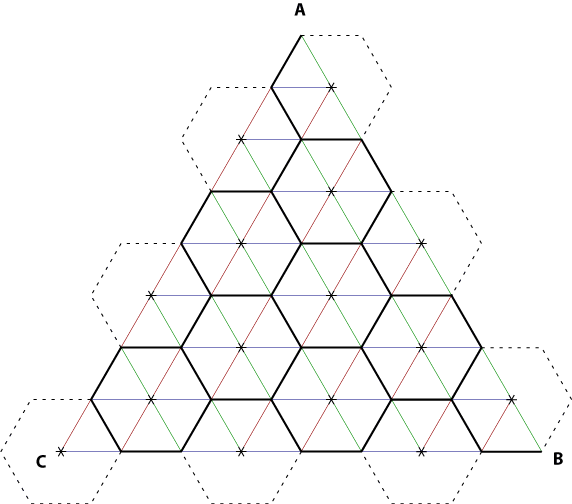
If we can find the center of each hexagon, we can add 6 faces for each hexagon (or less, if the hexagon falls off the edge of the main triangle). While there are various ways to traverse each hexagon, I take the lazy approach and use a recursive method, starting at point C.
- If the current hexagon's center is outside the bounds of the triangle, ignore it.
- If the current hexagon's center has already been processed, ignore it.
- Add the faces for the hexagon which have points inside the triangle.
- Find the three hexagons 'out' from the current hexagon, in the directions y_steps + 3, x_steps + 3, and x_steps + 1, y_steps + 1:
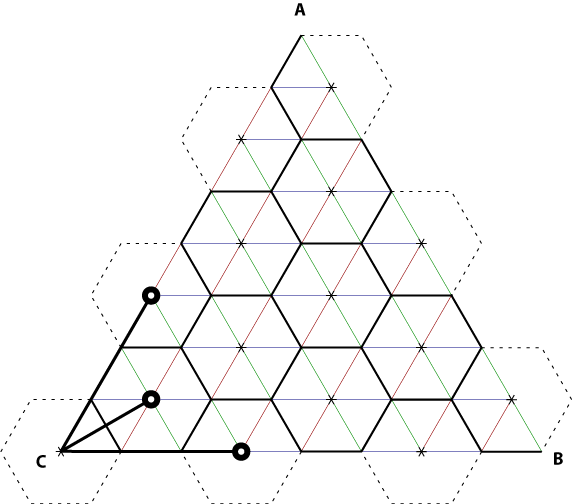
- Start back at step 1 with each of those three hexagons.
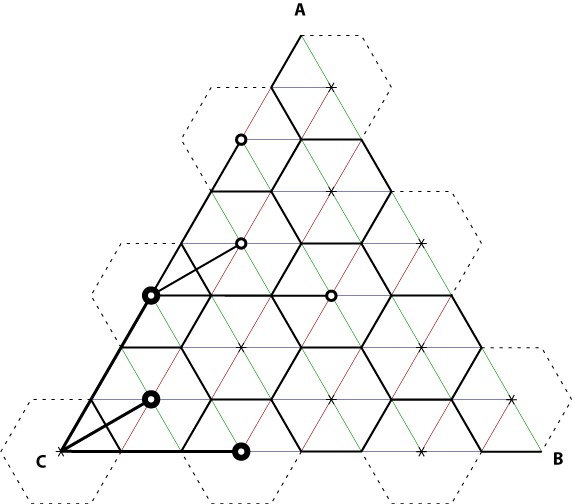
Step 2 is important, because the sloppy way we're traversing the hexagons means that we will hit some more than once. The following pretty-but-vapid diagram shows the order in which each hexagon is processed, from red to dark orange, light orange, yellow, green, cyan, blue, purple, and then magenta.
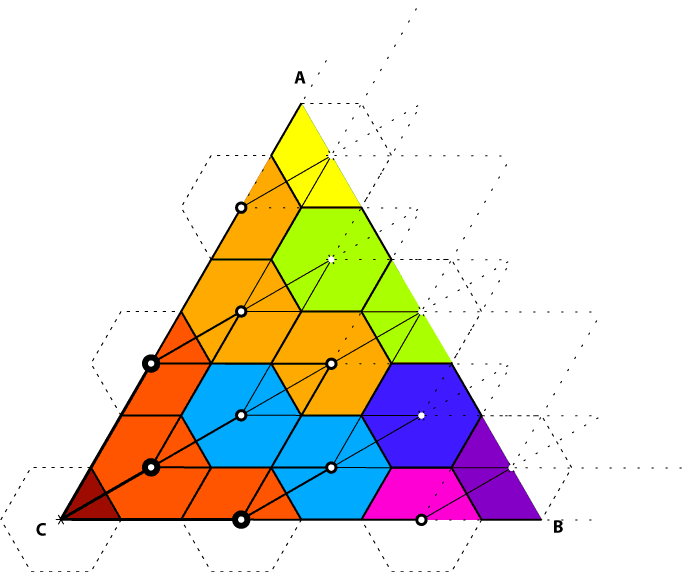
As previously noted, various (more sensible) approaches exist to find all the hexagons; better ones than described above would prevent any need to worry whether or not the hexagon had been processed before.
The final step is to find the point referred to by the offsets...
pt = C + x * x_steps + y * y_steps
...and then 'normalize' it, pushing the point out from the center of the geodesic sphere to the correct distance.
The Final Code
Following is the core Ruby code which takes a single face and subdivides it by an arbitrary frequency, returning an array of faces. Rather than re-creating For the more full-featured code—which provides the ability to calculate the normal of the face, determine if the normal is "in" or "out", reverse the face, and more—see the Geodesic.rb file.
# Represents a triplet of Vectors defining a face
class Face
attr_reader :a, :b, :c
def initialize( *pts )
@a, @b, @c = *pts.flatten
end
# Subdivide the face into (frequency+1)^2 sub-triangles
#
# Returns an array of new Face instances
#
# Note that the points shared by common faces will be pointers to the same vector instance
def subdivide_by( frequency=0 )
@freq = frequency
@x_offset = (@b-@c) / (frequency+1)
@y_offset = (@a-@c) / (frequency+1)
@sub_faces = []
@sub_points = {}
process_hex( 0, 0 )
@sub_points.each_value{ |v| v.normalize! }
@sub_faces
end
private
def process_hex( x_steps, y_steps )
return if seen_point? x_steps, y_steps
#skip this hexagon if the center isn't in bounds
hex_center = point_at( x_steps, y_steps )
return unless hex_center
# Find the 6 points around the hexagon
p1 = point_at( x_steps+1, y_steps )
p2 = point_at( x_steps, y_steps+1 )
p3 = point_at( x_steps-1, y_steps+1 )
p4 = point_at( x_steps-1, y_steps )
p5 = point_at( x_steps, y_steps-1 )
p6 = point_at( x_steps+1, y_steps-1 )
# Add the six triangles in the hexagon as faces
# but only if all points for the face are in bounds
@sub_faces << Face.new( p1, p6, hex_center ) if p1 && p6
@sub_faces << Face.new( p2, p1, hex_center ) if p2 && p1
@sub_faces << Face.new( p3, p2, hex_center ) if p3 && p2
@sub_faces << Face.new( p4, p3, hex_center ) if p4 && p3
@sub_faces << Face.new( p5, p4, hex_center ) if p5 && p4
@sub_faces << Face.new( p6, p5, hex_center ) if p6 && p5
# Process the 3 hexagons 'out' from this one
process_hex( x_steps+3, y_steps )
process_hex( x_steps+1, y_steps+1 )
process_hex( x_steps, y_steps+3 )
end
# Returns the Vector if the point referenced by the step
# offsets has already been visited/created; nil otherwise
def seen_point?( x_steps, y_steps )
@sub_points[ [ x_steps, y_steps ] ]
end
# Adds/returns the Vector object corresponding to the
# x/y offset steps from point c; nil if out of bounds
def point_at( x_steps, y_steps )
return nil unless in_bounds?( x_steps, y_steps )
@sub_points[ [x_steps, y_steps] ] ||= @c + @x_offset * x_steps + @y_offset * y_steps
end
# Returns true if the point referenced by the step offsets
# is in bounds for the overall face; false otherwise
def in_bounds?( x_steps, y_steps )
x_steps >= 0 && y_steps >= 0 && (x_steps + y_steps) <= (@freq+1)
end
end